Rekursive Funktionen
In der Mathematik ist die Verwendung von Rekursion zur Definition von Funktionen Gang und Gäbe. Eine typische Definition der Fakultätsfunktion sieht zum Beispiel so aus.
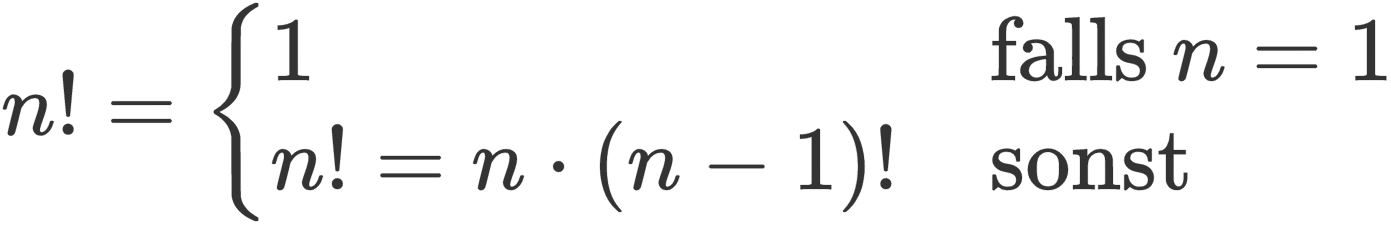
Diese Definition können wir mit Hilfe einer bedingten Verzweigung direkt nach Python übersetzen:
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
Falls der Parameter n gleich 1 ist, ist das Ergebnis ebenfalls 1. Falls nicht, wird das Ergebnis mit Hilfe eines rekursiven Aufrufs berechnet.
Rekursive Funktionen sind oft auf diese Weise strukturiert. Mit einer bedingten Verzweigung wird die Abbruchbedingung geprüft, die darüber entscheidet, ob die Berechnung beendet wird oder weiter geht. Im Fall, dass die Berechnung weiter geht, folgt ein rekursiver Aufruf, im Abbruchfall nicht. Falls die Abbruchbedingung nie erfüllt ist, terminiert die Berechnung nicht, genau wie bei einer bedingten Wiederholung, deren Bedingung immer erfüllt ist.
Um die Auswertung rekursiver Funktionen mithilfe von Programmausführungstabellen zu veranschaulichen, muss man für jeden Aufruf eine neue Tabelle anlegen.
Statt einer Funktion, die sich selbst aufruft, können wir auch Gruppen mehrerer rekursiver Funktionen definieren, die sich gegenseitig aufrufen. Die folgenden Definitionen illustrieren diese Technik:
def is_even(n):
if n == 0:
return True
else:
return is_odd(n-1)
def is_odd(n):
if n == 0:
return False
else:
return is_even(n-1)
Die Funktion is_even() liefert True oder False zurück, je nachdem ob die gegebene Zahl n gerade ist oder nicht. Sie verwendet dazu im rekursiven Fall die Funktion is_odd(), die ihrerseits is_even() im rekursiven Fall verwendet. Die Abbruchbedingung beider Funktionen testet, ob das Argument gleich Null ist. Für negative Eingaben definieren diese Funktionen deshalb nicht, was es heißt, gerade oder ungerade zu sein und ein Aufruf mit einem negativen Argument terminiert nicht.